在开始之前,我想解释几个基本术语,如方差(variance)、标准差(standard deviation)、估计值(estimate)、准确度(accuracy)、精度(precision)、平均值(mean)和期望值(expected value)。
我想本教程的许多读者都熟悉基本统计学知识。但是,在本教程的开头,我承诺提供理解卡尔曼滤波器操作所需的必要背景知识。如果您熟悉这个主题,可以跳过它。
- 平均值与期望值
虽然平均值(mean)与期望值(expected value)是密切相关的术语。但是,它们是不同的。
例如,假设有五种不同的硬币——两个5美分的硬币和三个10美分的硬币,我们可以通过平均硬币的价值来轻松计算硬币的平均值。
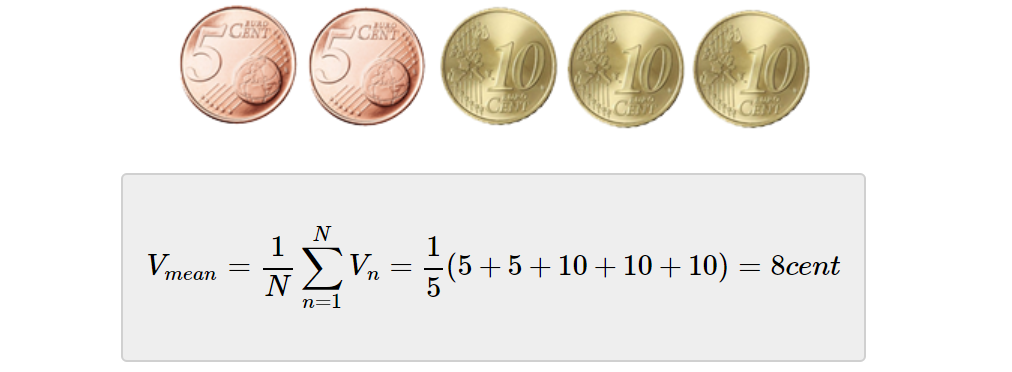
上述结果不能被定义为期望值,因为系统状态(硬币值)没有被隐藏(想要表达的是确定的,此处没有任何不确定性),我们已经使用了所有的population(所有5枚硬币)来计算平均值。
译者补充:因为很多同学经常混淆平均值与期望值的概念,因此,我在此特别解释一下。在解释两个概念之前,先说一下“大数法则”。
- 先说一下大数法则:

- 思考一下为什么会用到期望值?


期望值也就是每个数*对应的概率值,再求和
译者补充完毕。
现在假设同一个人的五个不同的体重测量值:79.8kg,80kg,80.1kg,79.8kg和80.2kg。
由于秤的随机测量误差,称重测量值不同。 我们不知道准确的重量值是多少,因为它是一个隐藏变量Hidden Variable。 但是,我们可以通过平均尺度测量来估计重量。 (准确测量值不可知)

估计的结果是体重的期望值。
平均数经常使用希腊字母:μ
期望值使用字母:E
- 方差与标准差
方差用来度量随机变量与其期望值(即随机变量的期望值)之间的离散程度。
标准差是方差的平方根。标准差: ,方差:
例如,我们想比较两个高中篮球队的身高。下表提供了两支球队的球员身高及其平均值。

如我们所见,两队的平均身高是一样的。现在让我们检查一下高度变化height variance。
由于方差用来度量随机变量与其期望值(即随机变量的期望值)之间的离散程度,我们想知道数据集偏离其平均值的情况。我们可以通过从每个变量中减去平均值来计算每个变量与平均值之间的距离。
我们将用x表示高度,用希腊字母μ表示高度的平均值。每个变量与平均值的距离为:

下表给出了每个变量与平均值之间的距离。

下表给出了每个变量与平均值的平方距离。
有些值是负数。为了消除负值影响,让我们将高度与平均值的距离平方:
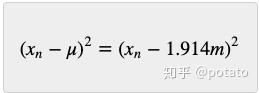

为了计算数据集的离散程度,我们需要从中找出所有平方距离的平均值:
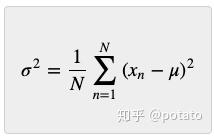
A队的方差是:

B队的方差是:

我们可以看出,虽然两队的平均值相同,但A队的身高分布值高于B队的身高分布值,这意味着A队在控球员、中锋和后卫等不同位置有不同的球员,而B队球员则技能相差无几。
方差的单位是平方的;查看标准差更方便。正如我已经提到的,标准差是方差的平方根。
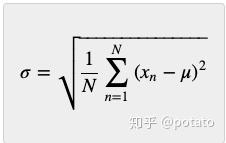
A队运动员身高的标准差为0.12米。
B队运动员身高的标准差为0.036米。
进一步的,现在,假设我们要计算所有高中篮球运动员的平均值和方差。这是一项非常艰巨的任务,我们需要收集所有高中运动员的数据。
但是,我们可以通过选择一个大的数据集并对这个数据集进行计算来估计参与者的平均值和方差。(样本估计全局)
随机选取的100名选手的数据集足以进行准确的估计。
然而,当我们估计方差时,方差计算公式略有不同。我们不用N因子归一化,而是用N - 1因子归一化:

你可以在以下资源中看到这个方程的数学证明:http://www.visiondummy.com/2014/03/divide-variance-n-1/
- 正态分布
事实证明,许多自然现象服从正态分布。继续以篮球运动员身高为例,如果随机选取运动员,构建大数据集,绘制身高VS.身高(heights vs. heights)的频率曲线图,得到“钟形”曲线,如下图所示:
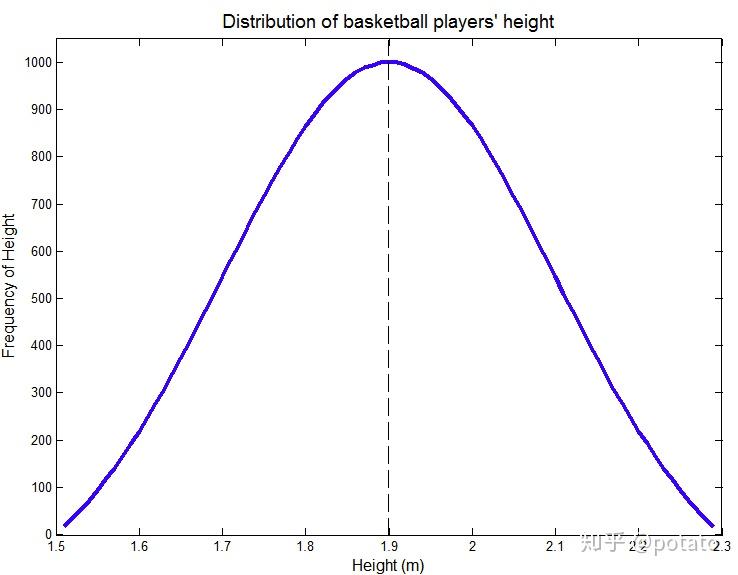
正如你所看到的,这条曲线关于平均值(平均值是1.9米)对称。平均值附近值的频率高于远处值的频率。
高度的标准差等于0.2米。68.26%的值在平均值的一个标准差内。如下图所示,68.26%的值介于1.7米和2.1米之间(绿色区域占曲线下总面积的68.26%)。
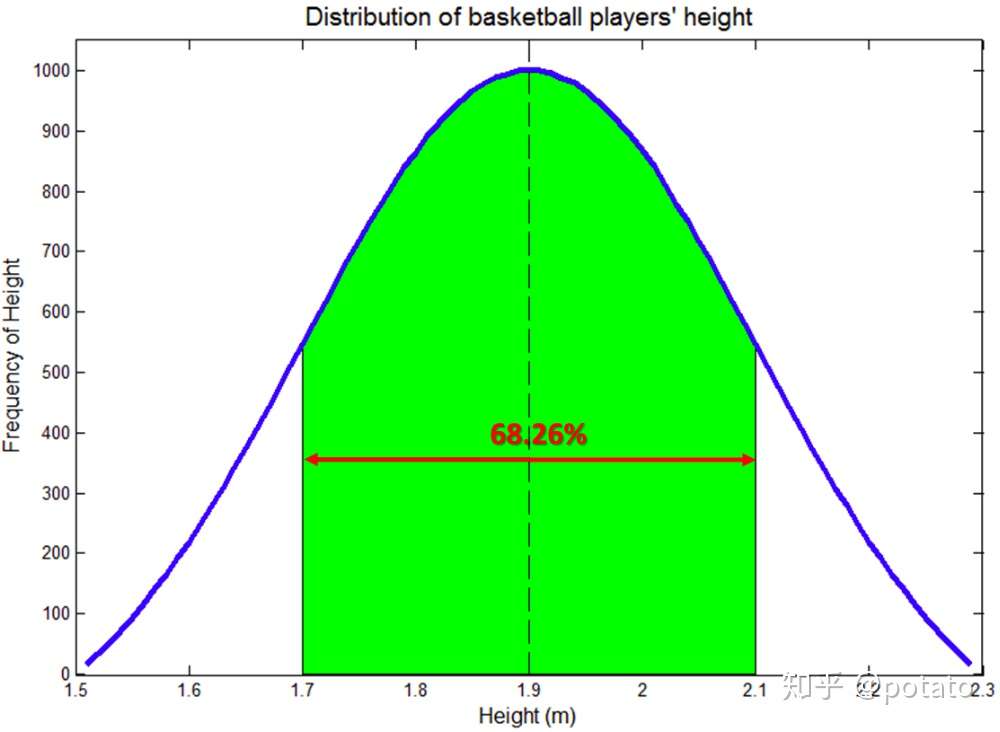
95.44%的值在距离平均值的两个标准差内。
99.74%的值在距离平均值的三个标准差内。
正态分布,也称为高斯分布(它以数学家Carl Friedrich Gauss的名字命名),由以下方程描述:
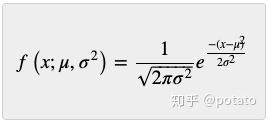
通常,测量误差是正态分布的,因此卡尔曼滤波器设计基于测量误差是正态分布的假设。
- 估计、准确度与精度
— 估计(Estimate):评估系统的隐藏状态。飞机的真实位置对观察者来说是隐藏的。我们可以用雷达等传感器来估计飞机的位置。采用多传感器和先进的估计跟踪算法(如卡尔曼滤波),可以显著提高估计精度。每一个测量或计算参数都是一个估计值。
— 准确度(Accuracy):表明测量值与真实值的接近程度。
— 精度(Precision):描述同一参数的许多 度量值中有多少可变性。准确度和精度是估算的基础。
下图说明了准确度和精度。
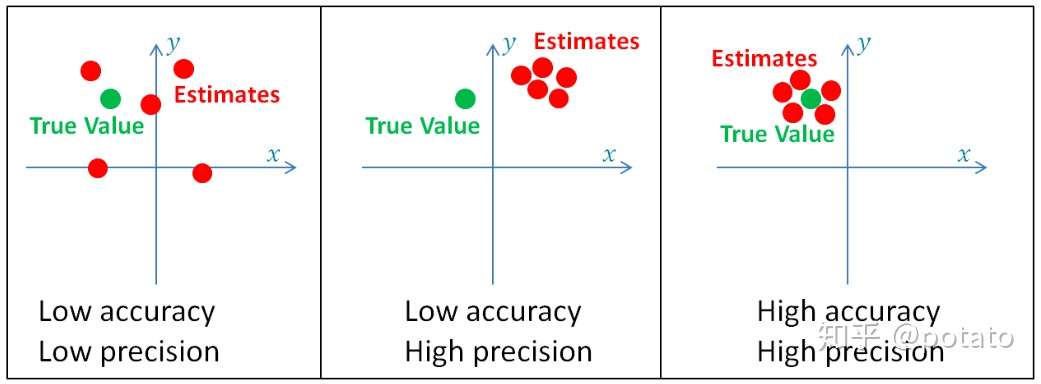
高精度系统的测量方差较低(即不确定度/离散程度/变化程度较低),而低精度系统的测量方差较大(即不确定度/离散程度/变化程度较高)。方差是由随机测量误差产生的。
低精度系统被称为偏差系统,因为它们的测量具有内置的系统误差(偏差)。
通过平均或平滑测量可以显著降低方差的影响。例如,如果我们使用一个具有随机测量误差的温度计来测量温度,我们可以进行多次测量并对测量的值进行平均。由于误差是随机的,所以有些测量值会高于真实值,而另一些测量值会低于真实值。我们做的测量越多,估计就越接近。
另一方面,如果温度计有偏差,估计将包括一个恒定的系统误差。
本教程中的所有示例都假定系统是无偏差的。

极小化性能指标: 最优解

J就是选择能够令方差 最小的的参数。 X^就是最优解
