前言
近日,旷视上海研究院长危夷晨在将门技术社群做了一次题为《Uncertainty Learning for Visual Recognition》(不确定性学习在视觉计算中的应用) Online Talk,共分为4个部分:
- Preliminary(基础知识)
- Uncertainty in Deep Learning(深度学习中的不确定性问题)
- Uncertainty in Computer Vision(不确定性的计算机视觉应用)
- Summary(总结)
我主要参考了前三部分的内容
基础知识
何为不确定性估计
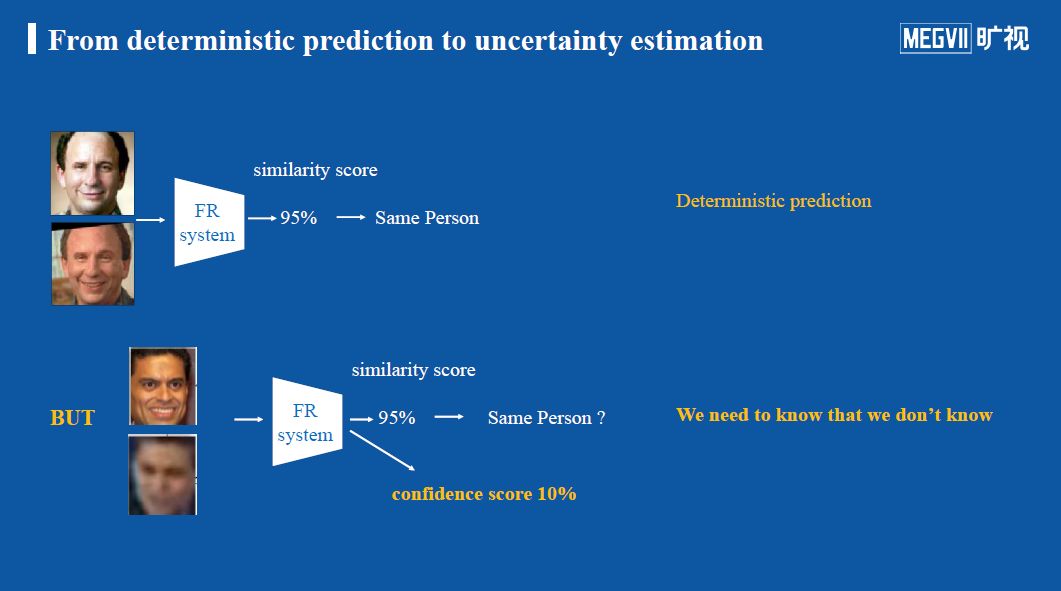
要理解何为不确定性估计,我们可以先从确定性预测(deterministic prediction)开始。假设要对两张人脸进行对比,验证是否是同一个人的照片,那么可以使用人脸识别系统分别对这两张人脸图片提取特征,并使用某种度量指标衡量所提取的两个特征的相似程度,根据所预测出的相似程度来判断两张人脸图像是否从属同一个人。如果相似度很高(比如95%),则可以判断这两张人脸属于同一个人。这种通过预测一个确定性的人脸特征用来判断的方式被称为确定性预测(deterministic prediction)。
然而这个相似度分数并不总是有效,以下图中第二个例子为例,可以看到在输入图像中,一张非常清晰,另一张十分模糊,然而这个时候人脸识别系统依然给二者打出很高的相似度分数,那么面对这种情况,我们是否要相信系统给出的答案,我们是否有办法来判断系统给出这个分数的可靠程度?
为此,人们提出了另一个辅助判断的指标,即判断机器给出的答案是否可信,可信程度多少的分数被称为confidence score(置信度分数)。如下图第二行中,系统给出相似度95%,然而confidence score却只有10%,表明系统给出的相似度分数的可信度很低,因此我们在采纳系统给出的这个判断答案的时候需要十分谨慎。
从这个案例可以知道,在confidence score分数背后存在一个核心思想,即很多时候机器学习系统给出的判断不一定是靠谱的,即,系统对于给出的判断具有一定程度的“不确定性”。那么此时人们就需要知道系统给出这个判断到底有几成把握,因此我们需要诸如置信度分数或者“不确定性”分数这样的额外信息来帮助我们做出更好的决策。
为何不确定性重要
上面介绍完之后,我们再来谈谈它为什么重要。简单来讲,不确定性估计在深度学习之中有着广泛的应用场景,为其落地发挥着不可替代的重要作用,下面讲一些比较要代表性的场景:
- 高风险应用场景。这类场景需要非常精确的估计,因为一旦估计错误,可能出现严重的后果,例如医疗图像诊断、自动驾驶。
- 大量机器学习场景。比如,在主动学习(Active Learning)这种技术框架中,模型需要确定哪些样本更值得被打标签。这也涉及到系统对于估计样本“价值程度”不确定性。同时,研究人员往往也会发现单纯使用机器学习系统进行判断时,会存在少量样本系统无法做出很好的判断,因此这时人们会邀请专家来标记这部分困难样本,以训练模型。
- 强化学习。强化学习由于经常要权衡exploration和exploitation操作,因此如何确定每一台机器的概率分布是否被准确估计,就是对这台机器模型参数的不确定性估计。
- 对处于训练数据分布之外情况的检测。由于很多时候测试数据并不在训练数据中,因此如果测试数据超出了训练数据的数据分布,那这样的预测是没有准确度可言的,这时候就需要一个额外的不确定性估计来确认对当前的预测有多大把握。
两种不确定性
接下来,我们界定一下不确定性的分类问题。一般来讲,不确定性可以分为两类:
- 数据的不确定性:也被称为偶然(Aleatoric)不确定性,它描述的是数据中内在的噪声,即无法避免的误差,这个现象不能通过增加采样数据来削弱。例如有时候拍照的手稍微颤抖画面便会模糊,这种数据是不能通过增加拍照次数来消除的。因此解决这个问题的方法一般是提升数据采集时候的稳定性,或者提升衡量指标的精度以囊括各类客观影响因素。
- 模型的不确定性:也被称为认知(Epistemic)不确定性。它指出,模型自身对输入数据的估计可能因为训练不佳、训练数据不够等原因而不准确,与某一单独的数据无关。因此,认知不确定性测量的,是训练过程本身所估计的模型参数的不确定性。这种不确定性是可以通过有针对性的调整(增加训练数据等方式)来缓解甚至解决的。
深度学习中的不确定性问题
如果单看深度学习网络本身,它是确定性的,例如简单的多层前馈网络,在训练好以后,其结构、权重以及对某一个样本所输出类别的概率都是确定的。因此,在深度神经网络中引入不确定性的一个方法就是引入贝叶斯法则,从而得到贝叶斯神经网络(BNN)。
简单而言,如下图,贝叶斯神经网络的权重不像普通神经网络是一个具体数值,而是一个概率分布,表示每一个权重w遵循一个分布,而非之前是一个确定的数值。因此在训练和推理中,网络的权重会变化,根据分布来随机采样。通过这种方法可以建模各个参数本身存在的不确定性。
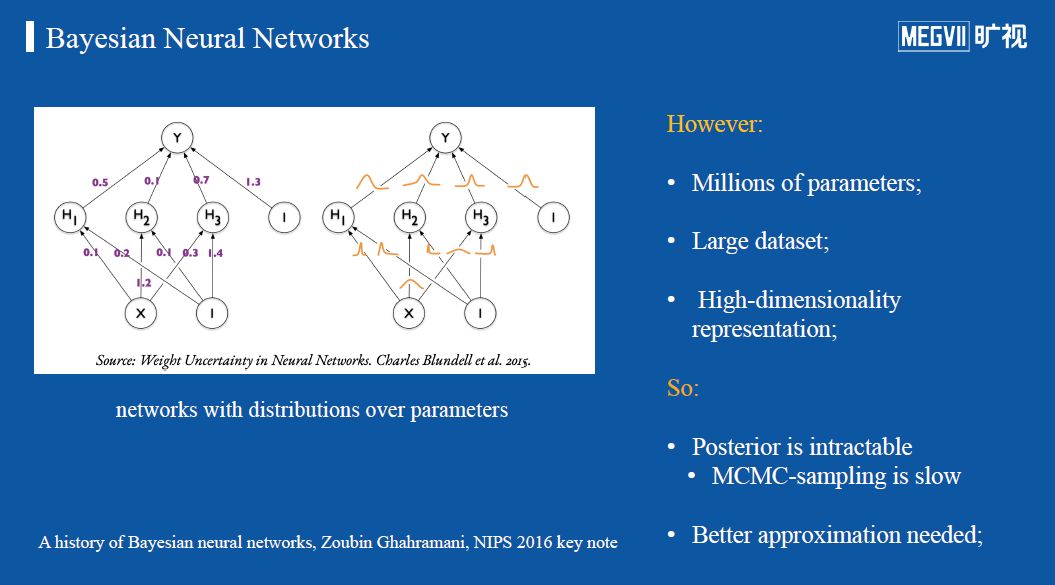
然而,由于在实际应用中参数量十分巨大,要严格根据贝叶斯公式计算后验概率几乎不现实,因此为了将网络应用于大型数据集,就需要高效的近似计算方法。早期比较有名的方法是通过马尔科夫链蒙特卡洛采样法(MCMC-sampling)来逼近假定的参数分布,但是由于这种方法很慢,因此发展出了一系列更好的近似计算后验概率的方法,如下:
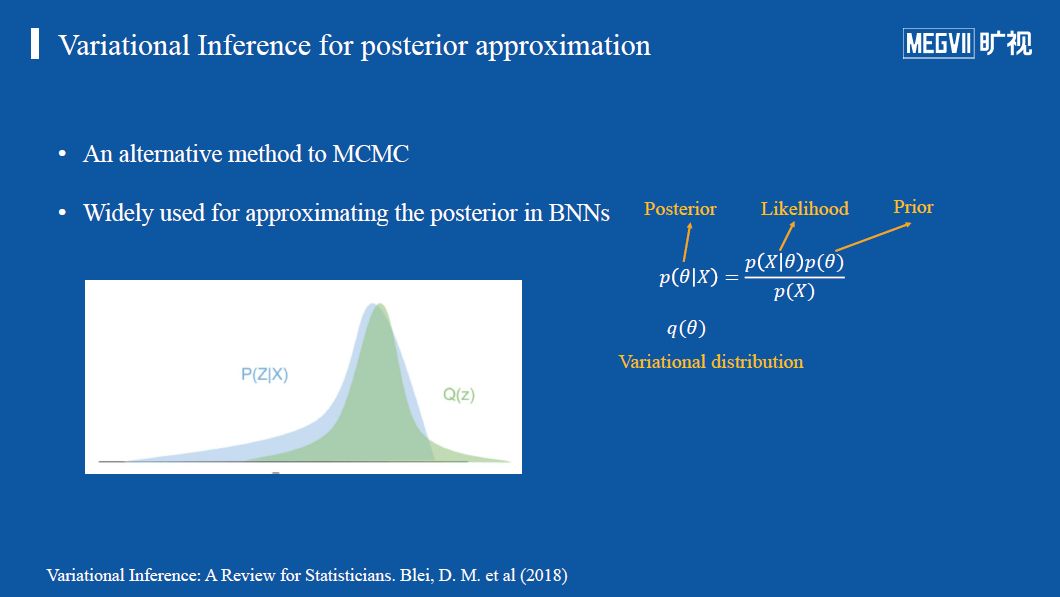
变分推断
变分推断的基本方法就是引入变分分布对BNN优化过程中涉及到的后验概率进行近似估计,这种方法较为高效。
Dropout=BNN+VI

这种dropout方法也称为蒙特卡洛dropout,进一步简化了对后验概率分布的近似计算,它认为常见的dropout技术实际上等于在贝叶斯网络中进行变分推断。通过上图的对比,我们可以直观理解标准神经网络经过dropout之后,在每一层随机取消一些神经元,把连接变稀疏的网络是什么样子。
可以证明,在假设每一个神经元都服从一个离散的伯努利分布的情况下,经dropout方法处理的神经网络的优化过程实际上等价于在一个贝叶斯网络中进行变分推断。由于这种结构中每个节点的权重是被多个子网络共享的,因此它的训练和推理相对高效。这项理论成果近年来得到了较多的应用。
我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作(每一个批次都是随机),这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征。
dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
Dropout具体工作流程
假设我们要训练这样一个神经网络,如图所示。
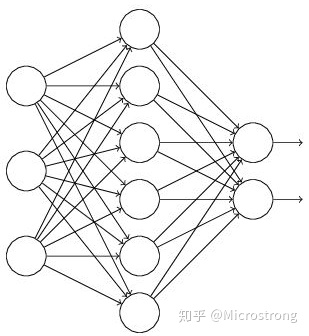
输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后,过程变成如下:
(1)首先随机(临时)删掉网络中一半(dropout=0.5时)的隐藏神经元,输入输出神经元保持不变(图中虚线为部分临时被删除的神经元)
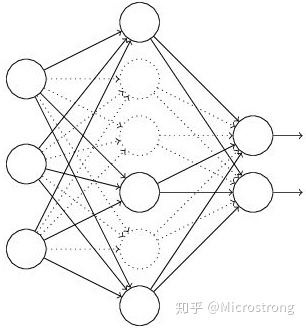
(2) 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
(3)然后继续重复这一过程:
- 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
- 对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数(w,b) (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
不断重复这一过程。
参考
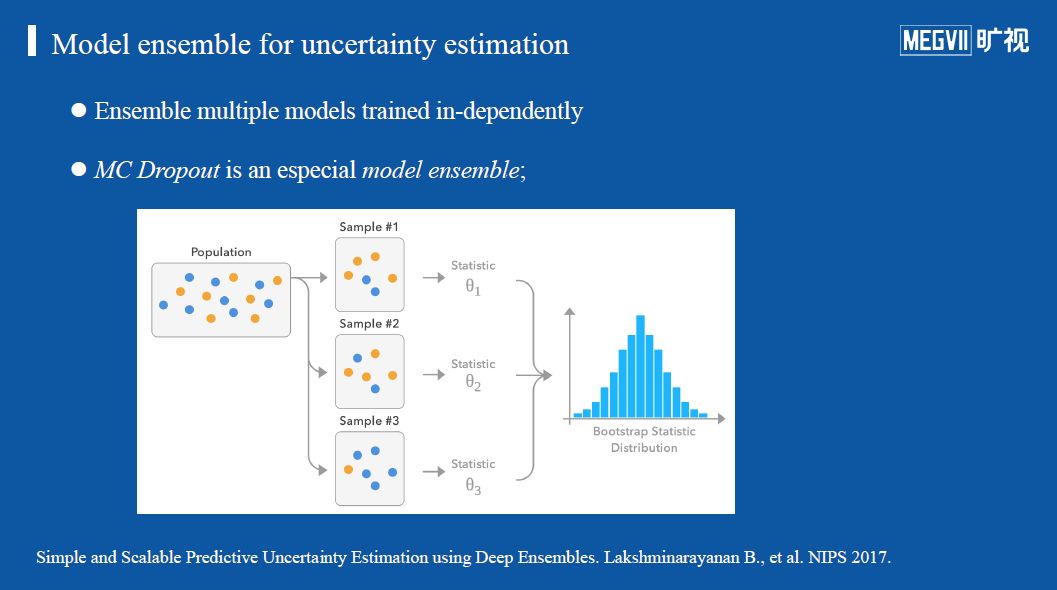
模型融合
这也是一种进行不确定性估计的基本方法,其大致思路是,从一个数据集中进行多次随机采样,分别训练模型,然后再将这些模型的推理结果综合,其均值作为预测结果,方差作为预测的不确定性。另外需要强调的是,蒙特卡洛dropout可以认为是一种特殊的模型融合方法。
回归问题中的数据不确定性
这是一种数据估计的标准做法。给定输入x_i,解一个函数f(x_i),使得它逼近ground truth y_i。假设这个函数f(x_i)遵循一个高斯分布,那么其均值就是y_i,方差就是σ(也依赖于x_i)。
这时,如果对这个高斯分布取似然度,再取负的log值,那么就可以得到下图中的损失函数L。因此在优化的时候,除了希望优化f(x_i)逼近y_i,同时也需要优化σ(x_i),它表示这个高斯分布的不确定性,σ越大越不确定。
因此当f很容易逼近y的时候,那么公式中第一项L2范数就会很小,这时即便σ也小,但结果依然不会很大;当f很难逼近y,即f很难学习的时候,第一项中的L2范数就会很大,这时优化过程就会使得σ也变大,从而使得整个第一项减小,因此学到的σ会随着数据学习的难度做自我调整。

简单例子
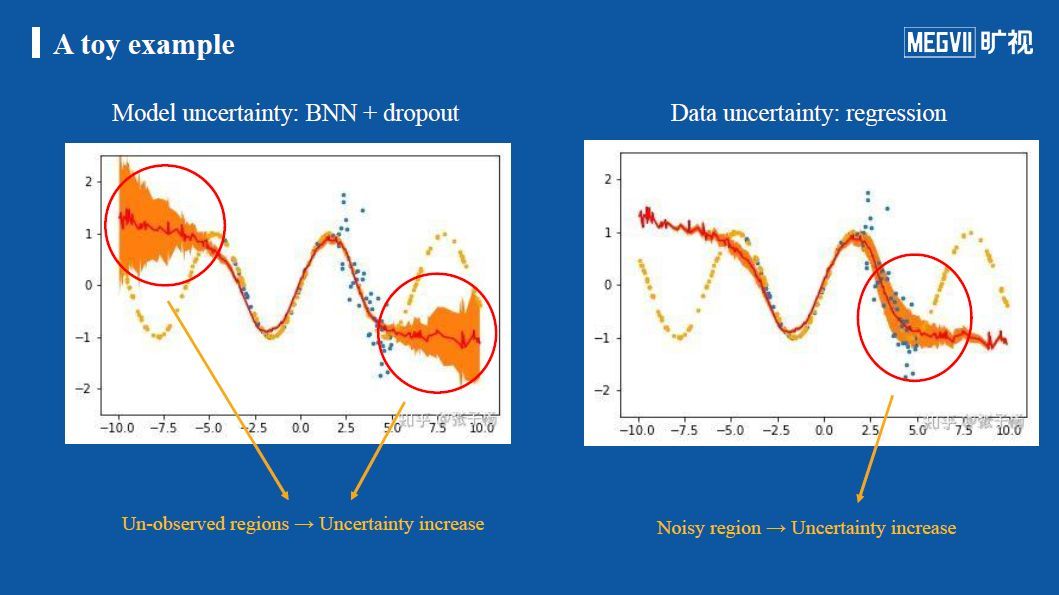
我们借助一个直观例子来理解模型不确定性与数据不确定性。首先这里的ground truth函数为一个正弦函数,即图中橙色的点是测试数据,而训练数据是从[-5,+5]区间采样的蓝色点,研究人员对每一个蓝色点都添加了高斯噪声,因此可以看到这些蓝色点明显偏离ground truth。
下方左图是用贝叶斯网络加dropout进行的模型不确定性估计。红色曲线为估计出来的预测值,延其上下分布的黄色面积则为每一个点对应的方差。在进行模型不确定性估计时,系统会对每个输入点估计多次,每次会随机采样模型的权重,以求出对每个输入点多次预测所得到的均值和方差。可以发现,蓝色点区域之外的部分预测的方差很大,这是因为模型没有见过这样的数据。(因为蓝色是训练数据,其它是测试数据,没见过的,所以方差就会较大,也就是不确定性较高)
下方右图中红色曲线为估计出来的预测值,是数据不确定性估计,曲线上下的黄色跨度就是每一个点通过数据不确定性估计方法所学出的方差。可以发现,原本输入数据中有噪声的部分,其预测出的方差比较大,反映出模型对这样的输出拥有较大的不确定性。
不确定性的计算机视觉应用

尽管不确定性在机器学习中已经有很长历史,但是直到2017年(就我所知)随着NeurlPS论文What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision的提出,它才开始真正应用在基于深度学习的视觉预测任务中。这篇论文本身没有太多方法创新,通过将已知的方法 用于语义分割与深度回归任务,取得了不错的结果。通过在模型中引入不确定性估计的已有理论成果,使得原本任务的精度得到了显著提升。
通过论文给出的定性结果可以较为直观的理解模型不确定性和数据不确定性。如下图,系统估计出来的不确定性是有明确含义即很容易理解的,图中上半部分做语义分割,下半部分做深度估计。
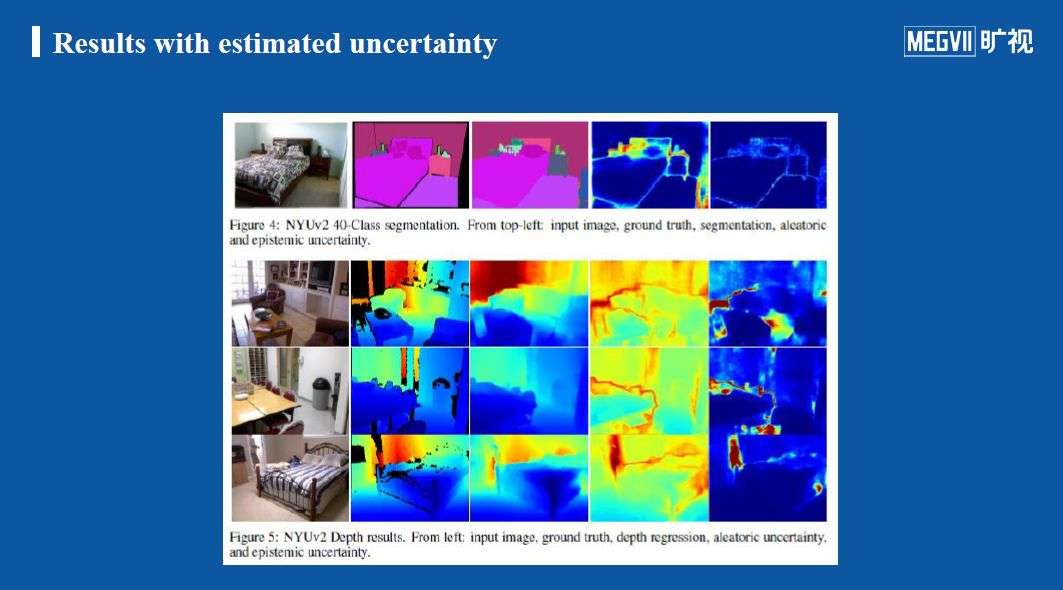
整张图的第4、5列分别是数据不确定性和模型不确定性的结果。红色部分表示不确定程度较大,蓝色部分表示较为确定。从数据不确定性结果(第4列)可以看到,红色部分往往出现在物体边界处,表示这些区域的像素更加具有二义性,系统不太清楚这部分像素究竟属于前景还是背景,另外这部分信息在训练数据中(即ground truth)往往也较模糊。可以发现,系统给出的数据不确定结果符合人类直观理解。
从模型不确定性结果(第5列)可以看到,模型对出现人的部分给出了很高的不确定性,这是因为模型在训练中很少遇到人的数据,因此模型很难估计出人所处位置的深度,将该区域标记为高度不确定。
物体检测中的数据不确定性

在物体检测任务中,很大一部分不确定性来源于标注数据的不确定。上图给出了几个典型例子,可以看到,在标注边界框的时候,由于存在各种物体角度、遮挡,所以往往很难评价一个边界框标注的好坏。由于标注规则不一、数据本身存在的各种不确定性,因此具有二义性的数据标注会导致具有二义性的学习结果,从而将不确定性引入了模型,进一步输出结果也是不确定的。
针对这个问题,有研究人员在CVPR 2019、ICCV 2019提出了两篇颇有价值的论文,其核心思想类似,将每一个边界框的4个坐标均认为呈高斯分布,然后分别估计其均值和方差。用上述介绍的数据不确定性回归公式来替代传统的L1损失,将原来所需要预测的4个变量扩充为8个变量。
因此,这种方法除了可以估计边界框每一个坐标之外,还让它们都带有了一个不确定性参数。利用这些不确定性数据,可以进一步做很多事情(比如在NMS中作为权重来对边界框位置进行投票)。
人脸识别中的模型不确定性
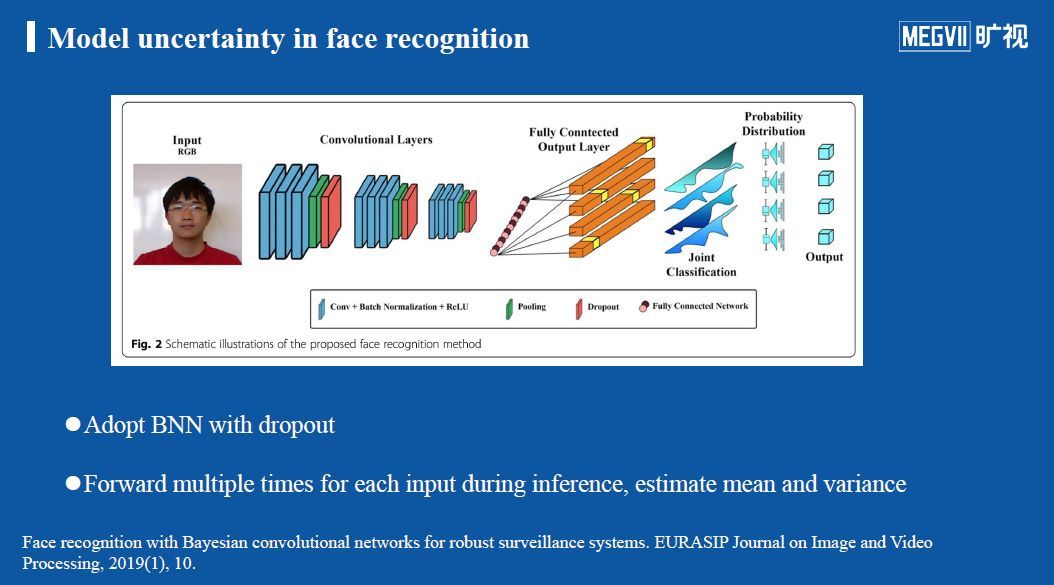
对于在人脸识别任务中如何估计模型不确定性,推荐大家上图中的论文工作,其核心思想是,将BNN+dropout用到人脸识别任务中,如图所示,dropout层(红色)被加在每一个卷积block之后,从而构建了一个蒙特卡洛Dropout网络。在训练过程中,每当流程到达这些层的时候,就会随机丢掉一些神经元,从而实现模拟参数分布的效果。在测试过程中,每一个图像都会经过该网络多次,进而可以多这些结果估计均值与方差,将方差作为预测结果的不确定性。
人脸识别中的数据不确定性:PFE方法
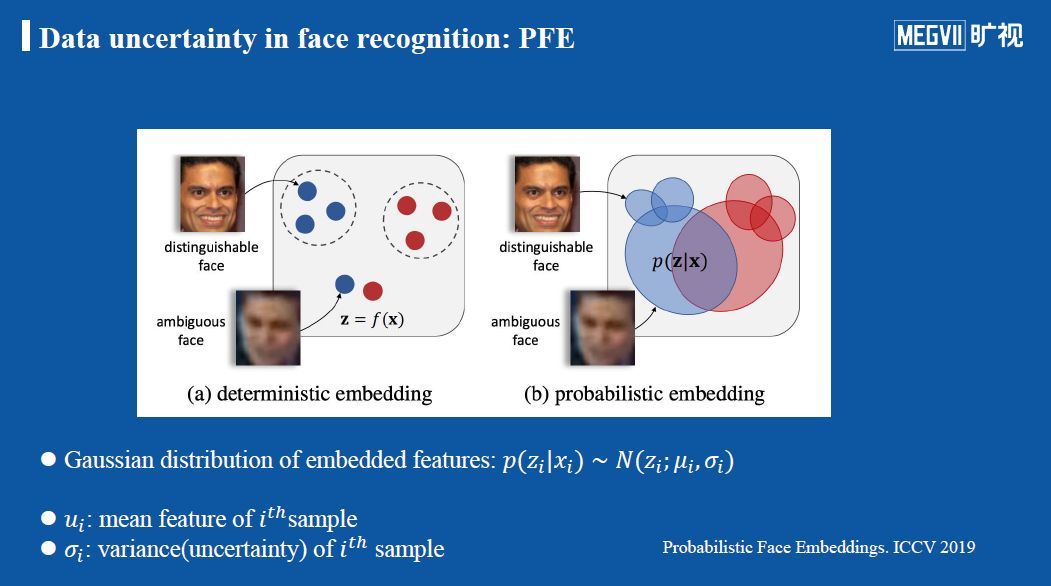
PFE方法全称为Probabilistic Face Embeddings,其核心思想是用概率分布来替代传统确定的人脸嵌入特征。传统的方法会将输入图像映射到一个高维空间中,得到一个表示特征的向量,然而对于这些方法而言,输出的向量都是确定的,因此被称为deterministic embedding。PFE引入了不确定性,将输出向量认为是一个概率分布,而不再是一个确定的向量,它有一个均值μ、方差σ。
均值代表对图像的嵌入,方差描述了模型对输入数据的不确定性。该方法希望同时估计μ和σ,并且σ能够根据输入图像的质量、包含噪声的程度进行自适应的学习。在上图右方的示例中可以看到,每一个输出的特征z不再是一个点,而是一个高斯形状的概率分布(椭圆),椭圆的大小就描述了估计的不确定性。

从具体实现方法来看,PFE的创新值得借鉴,它并不直接去估计每一个均值μ,而是通过一个事先已经训练好的人脸识别模型来抽取每个样本的特征μ_i,然后研究人员再在网络中加入一个小分支,来对每个样本输出一个方差(比如假设μ_i是一个512维的向量,那么此时也会输出一个对μ_i的每一维度单独估计方差的512维方差向量)。
进一步,论文提出了一种新的metric——mutual likelihood score(MLS),来衡量两个分布间的距离。上图公式中x_i和x_j是两个样本在特定空间中的高斯分布,两个分布所得到的MLS数值就代表了其相似度。在训练过程中,针对所有positive 样本,计算负的MLS数值作为损失,并最小化该损失目标函数,进而可以估计新增加分支(估计方差的分支)的参数。

上图是论文对方差的解释,较为直观。可以发现红框标注出来的(方差超过一定阈值)图片都是姿态有较大变化、模糊、或者有遮挡的图片,系统都认为它们识别起来有较大不确定性;而正面、高清的图片不确定性普遍较小。为了进一步验证学习出来的不确定性是否能够有效解释图像质量,PFE在下方左图中进行了有关在低质量图像之间使用传统cosine相似度计算是否可靠的研究。
研究人员对清晰图片添加了不同程度的噪声,蓝色线代表原图与模糊图之间的相似度分数,而红色代表两张来自不同ID的图随模糊程度的增加所计算的相似度。可以发现对于同一ID(蓝线),随着模糊程度增加,相似度也逐渐降低;而对于不同ID,随着模糊程度增加相似度却在增加。这说明依据该相似度可能会将两张来自不同ID的模糊图像错认为是同一张图。这一现象在其它很多论文中也同样被观测到。
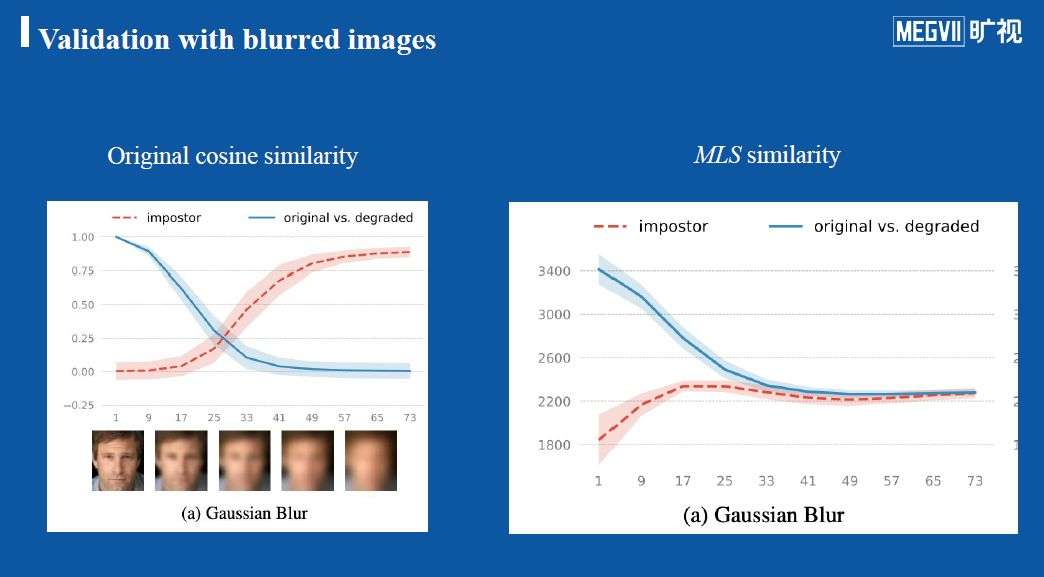
然而在经过PFE论文提出的MLS相似度修正之后,情况得到了很大改善。如右图,当图片模糊度增加时,对同样ID的图来说,其相似度没有变得太小,而不同ID图像的相似度也没有变得太大。这个实验证明这种计算图像相似度的新metric在面对低质量图片时更加鲁棒。
PFE方法的缺陷
虽然PFE方法取得了重要进展,但是缺点也很明显,因为它并没有学习身份特征(identity-feature),每一个identity的特征嵌入是确定的,PFE只是增加了一个估计方差的小网络分支,这导致必须用一个新的metric(即MLS)来计算所有样本对的距离。而使用MLS这个度量函数带来的缺陷在实际工业应用中是代价较高的:第一,我们需要额外存储方差向量;第二,相比传统的余弦相似度,MLS相似度的计算资源消耗也更大。
受此启发,我们团队在投递给CVPR 2020的新论文中不仅做到了估计方差,同时也能更新每个样本的特征。下图为传统方法、PFE与我们团队方法的对比。
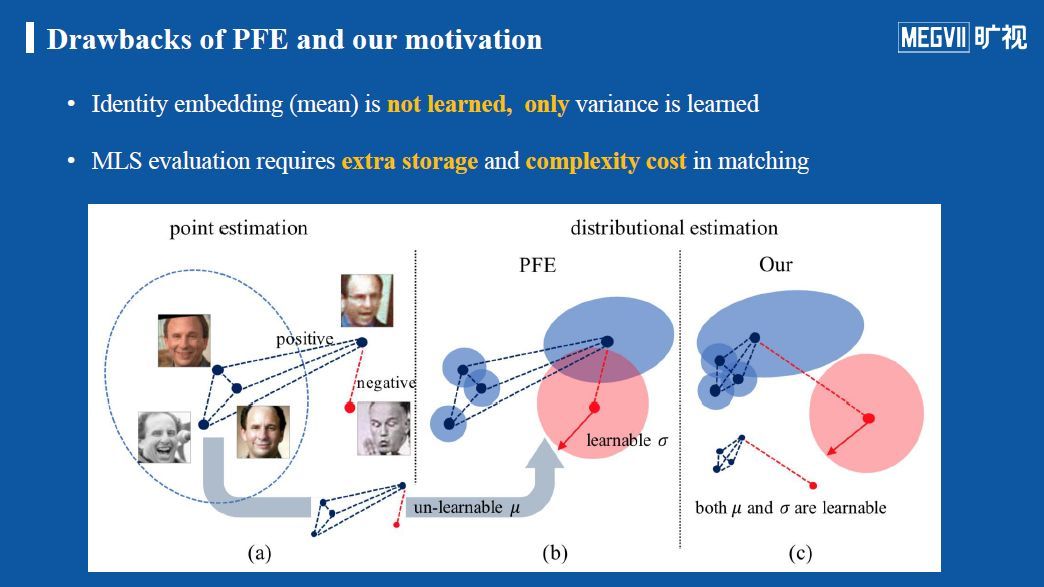
可以发现,在图(a)中,虚线框出的蓝色椭圆代表一个类别,圈外存在一个正样本和负样本,而对于传统相似度计算方法来说,很难将负样本和正样本区分开来;而(b)中PFE方法对每个样本估计了一个分布,在带有分布的特征表示下,利用MLS就能够有效将正样本和负样本区分开来,但是PFE中正负样本本身是确定的;在(c)中,我们团队方法能够在估计正负样本方差的同时,也让特征本身修正得更好。
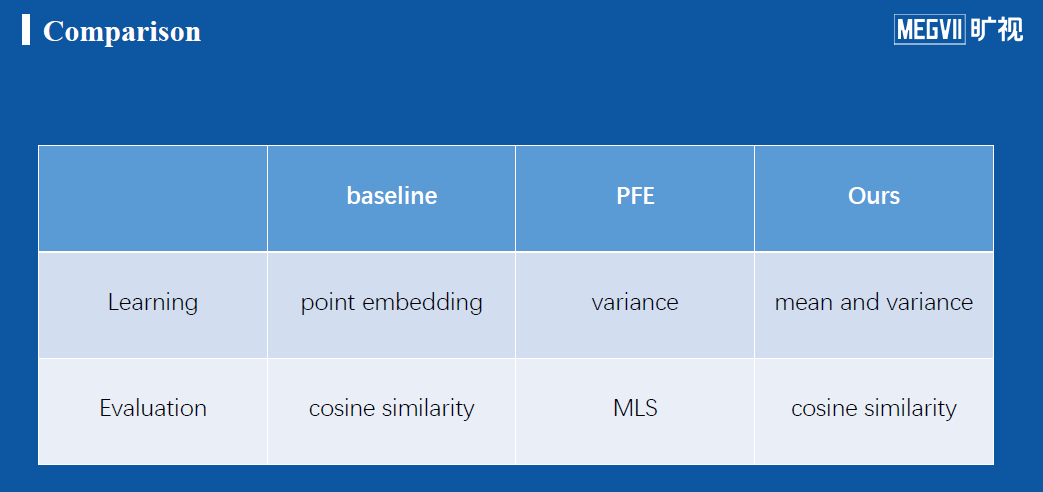
上图是三种方法的对比,可以看到在最后计算相似度的时候,由于特征本身经过了调整,只需要使用cosine相似度来计算两个均值向量就可以得出答案。具体而言,我们团队提出了两种实现方法,如下:
法1:从头学习一个分类模型
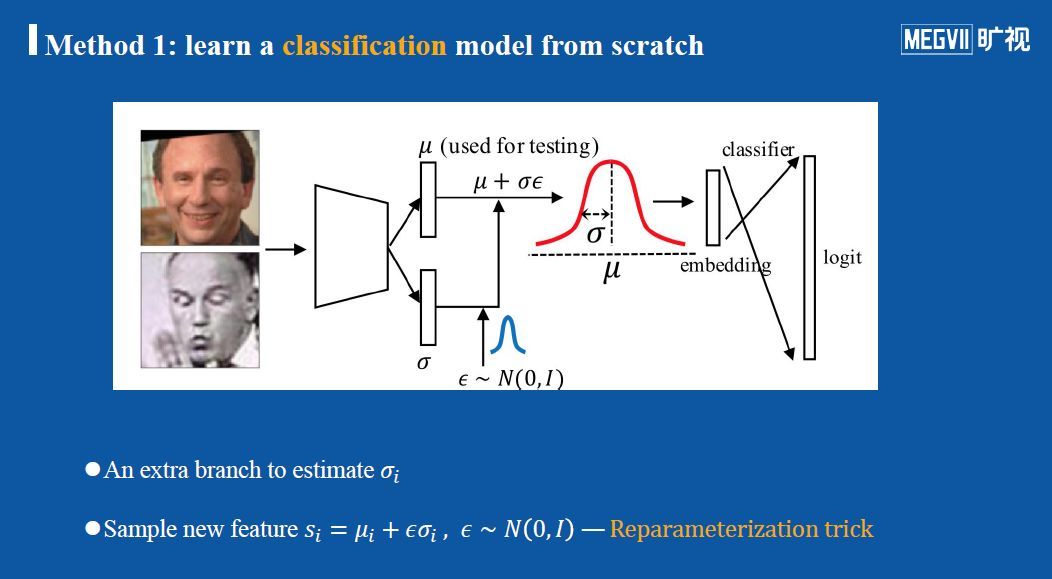
这种方法的主要部分与通用识别模型的结构一致,区别在于,在输出特征的位置,我们让模型输出一个有关每个样本特征的均值μ,以及一个方差σ。进一步,对于每个样本的每一次迭代而言,都随机采样一个ε(如上图最下方)。
通过这种方式得到的新样本特征s_i就是遵从均值μ、方差为σ的高斯分布采出的值,它可以模拟一个服从高斯分布的特征。通过这种简单的重新采样的技巧,就可以很好进行模型训练。在测试的时候不再需要采样,仅需要将已经得到的均值μ作为特征来计算相似度即可。

该方法的损失函数除了包含softmax以及其一切合理变种之外,还有一个KL损失,它使得每一个学出来特征的分布尽可能逼近单位高斯分布。这个损失项的引入来自于2016年一篇名为Deep variational information bottleneck的论文。进一步整个损失函数就可以用标准SGD方法来优化。下图解释了整个损失函数中softmax与kl损失是如何起到平衡的作用的。

法2:从现有模型出发学习回归模型
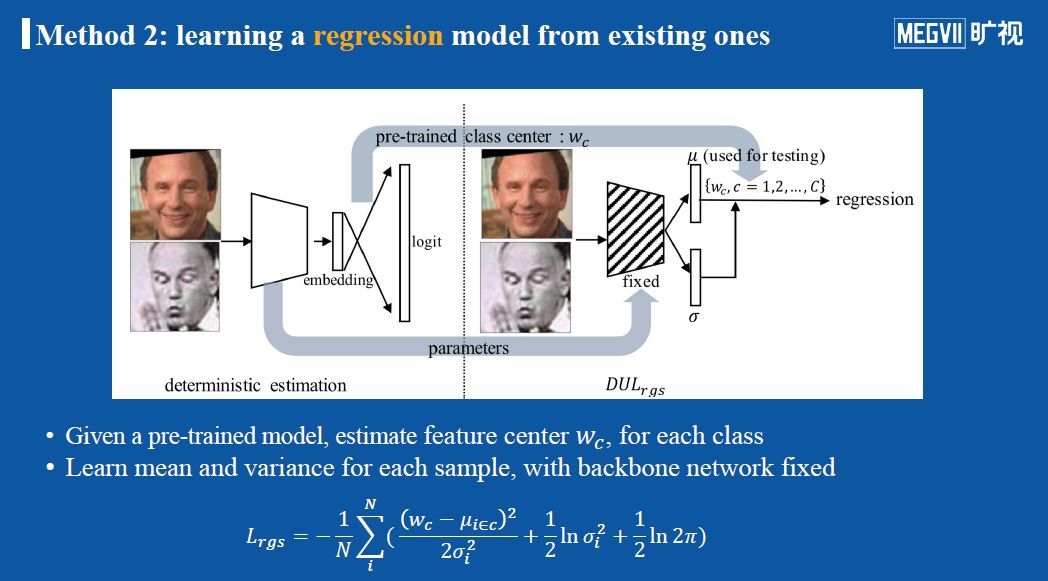
这种方法假设输出的特征μ遵循高斯分布,目的是让它逼近期望的特征w。与PFE类似,假设输入的模型已经固定,且输出的特征μ属于类别c,则让μ逼近这个类别c的特征中心w_c(w_c来自事先训练好的人脸分类模型)。这种方法适用于当已经有一个训练好的模型,但依然希望做不确定性估计的情况。相对于PFE而言,它多做了样本特征的学习。下图解释了该损失函数中σ起到的平衡作用。

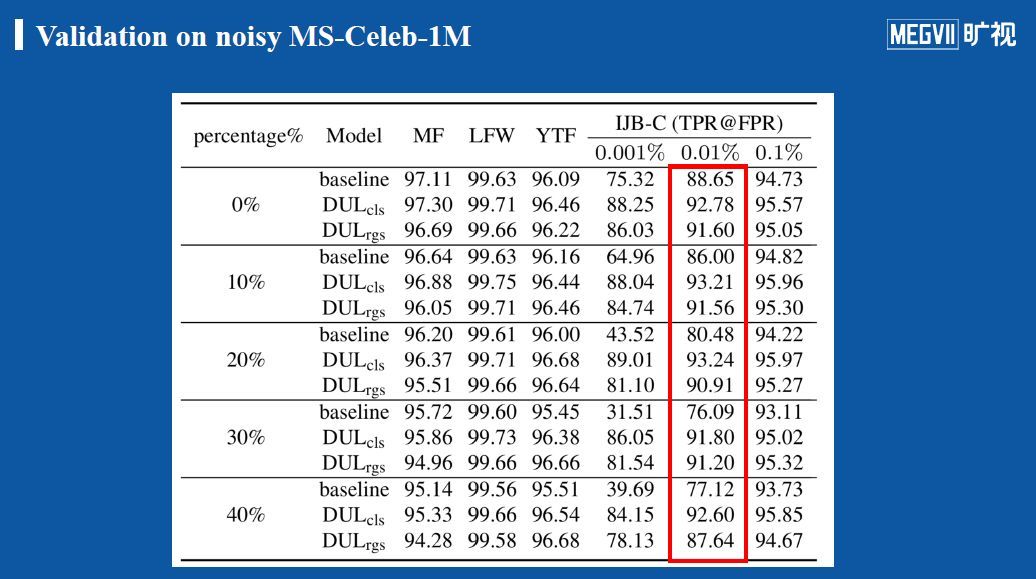
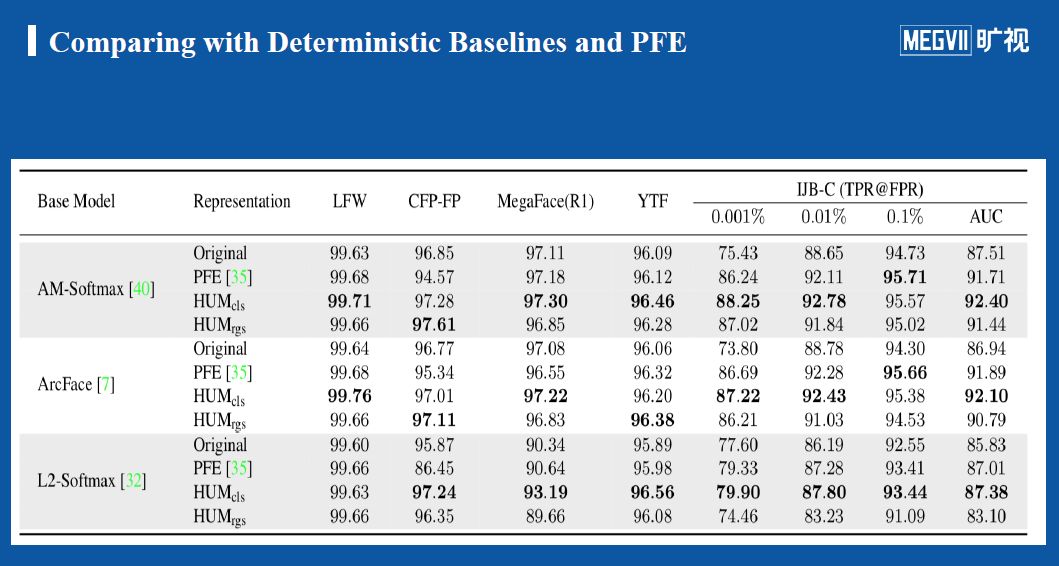
实验结果:在三种损失函数上的对比测试结果显示,我们团队提出的分类方法(HUM_cls)在最困难的数据集IJB-C(具有大量模糊、噪声图像)上效果最佳;在LFW、CFP-FP、YTF这些较成熟的数据集上我们提出的两种方法同其他方法区别不大;在较困难的MegFace(R1)数据集上我们团队的分类方法效果最佳。
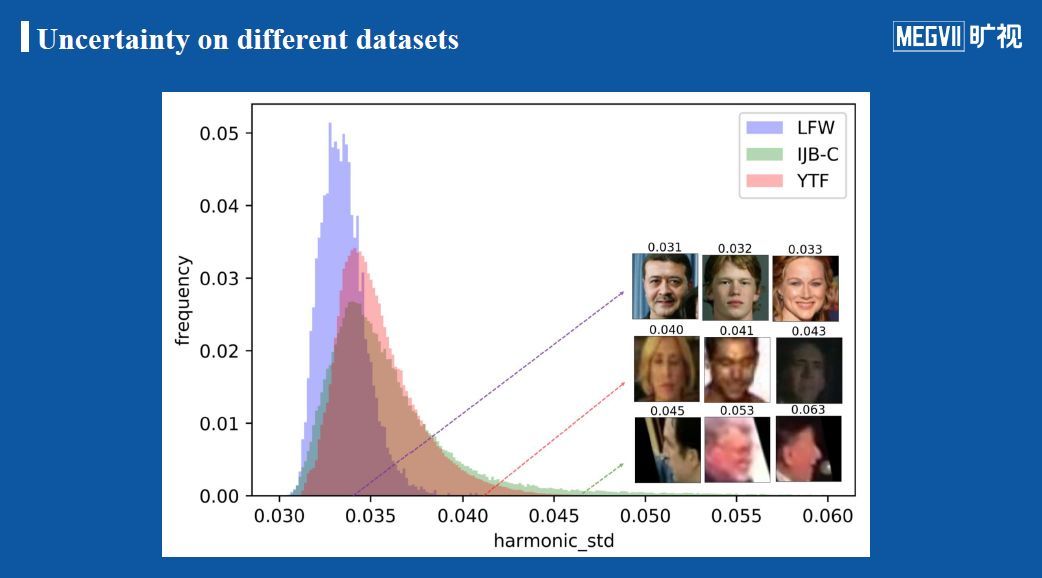
下图展示了在三种数据集上学习出来的方差分布情况,展示了位于不同方差位置的图像的样子。
进一步,我们团队使用了ResNet-64作为backbone(与PFE的SOTA模型backbone深度一致),来将本文方法同SOTA方法在最困难的数据集IJB-C上进行性能对比,结果显示在每一个指标上我们团队方法均实现了领先。为了测试本文方法对噪声信息干扰的鲁棒性,团队对图片人工施加了高斯噪声(从0到40%),可以发现,当噪声越明显的时候,本文引入的不确定估计方法的优越性也约高。